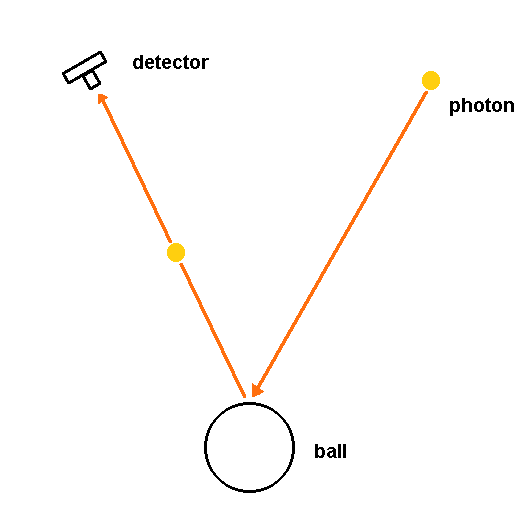
figure1
Because the flying ball is sufficiently slower than a photon, we can regard it standing still. So, when I shoot it, I get only a still image of it. This discussion can be generalized. Ordinarily, the moving object is enough bigger than a photon and it moves enough slower than a photon. So, we consider it as motionless. Hence, we can know only the position of the object as far as we detect a bounced photon.
The Motion is in Our Brain
Our eyes get only still images but our brain creates the motion picture from them. Donald Hoffman says that your brain creates the motion. He shows many examples in Visual Intelligence. Additionally, I represent one simple example. Figure 2-1 shows that there is a black circle at the left side. Figure 2-2 shows that there is a black circle at the left side. Figure 3 shows these two frames by turns. As a result, you may see the reciprocal movement of the black circle. However, there are only two still images. Furthermore, there is no motion of the black circle. Therefore, your brain creates the reciprocal movement of the black circle.
figure2
figure3
figure2
figure3
In astronomy, we can observe the position of a star at a certain time but we cannot directly observe the motion of the star. Hence, we need to calculate the trajectory of the star from observed data. Because the uniform linear motion is the simplest movement, we postulate the motion of the star between two points is the uniform linear motion. If a star has the circular orbit. Then, we can approximate it by the polygon. Figure 4 shows an example.
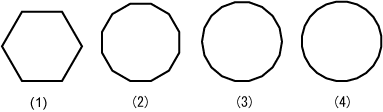
figure4
figure4
Consider that a star rotate in the circular orbit. If we know positions of it at six points, we approximate the circular obit by the hexagon. Figure 4-1 shows the regular hexagon. Figure 4-2, Figure 4-3 and Figure 4-4 show the regular 12-gon, the regular 18-gon and regular 24-gon, respectively. The regular polygon approaches the circle as the sides of it increase.
As seen above, any trajectory of a moving object is approximated by the collection of the uniform linear motion. So we can consider the uniform linear motion as the atom of the motion. Because our eyes can get only the position of the object at a certain time, our brain need to construct the trajectory of it from the collection of the uniform linear motion. Furthermore, we can know only the position of the object using any equipment, which detects the photon. Hence, we must presume the trajectory of the moving object. At that time, the uniform linear motion plays the role of the atom of movement.
As seen above, any trajectory of a moving object is approximated by the collection of the uniform linear motion. So we can consider the uniform linear motion as the atom of the motion. Because our eyes can get only the position of the object at a certain time, our brain need to construct the trajectory of it from the collection of the uniform linear motion. Furthermore, we can know only the position of the object using any equipment, which detects the photon. Hence, we must presume the trajectory of the moving object. At that time, the uniform linear motion plays the role of the atom of movement.
The Average Speed Is the Elemental Concept
Let us consider the equation of the uniformly accelerated motion:
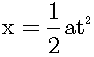
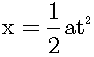
Because above equation is constructed from the collection of the uniform linear motion, we shall decompose it into the uniform linear motion. We shall regard the movement from time t to time t+Δt as the uniform linear motion. Then, figure 5 shows the distance-time graph of the decomposed uniformly accelerated motion from time 0 to time b.
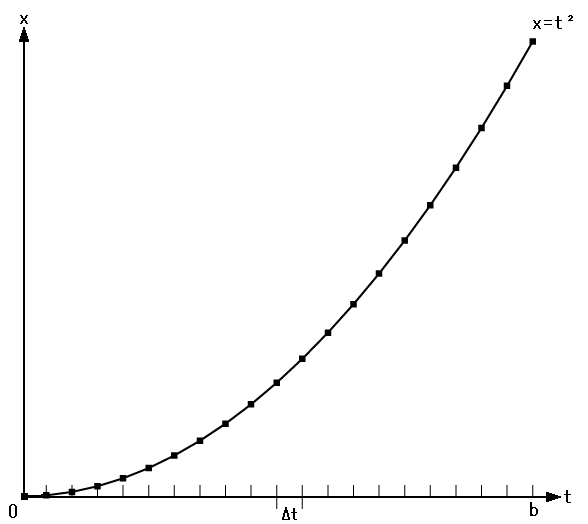
Figure5
Figure5
If we want to get the data for the graph, we need to shoot still images of the object in the continuous shooting from time 0 to time b. The graph shows the position of it in each shot, and the interval of the shots is ∆t. Next, let us calculate the average speed of it in the interval.
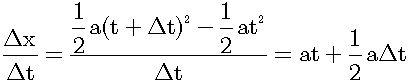
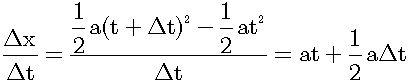
In the case of the uniform linear motion, above equation equals the speed of the motion. However, if the motion isn't the uniform linear motion, the above equation means the average speed of the interval between time t and time b+Δt. Because Δt is the small constant in the above equation, the division is clearly possible. So, we approximate the uniformly accelerated motion from time t to time t+Δt by the average speed uniform linear motion.
Next, we shall consider the relationship between the average speed and the integral. Figure 6 shows the velocity-time graph of the uniformly accelerated motion.
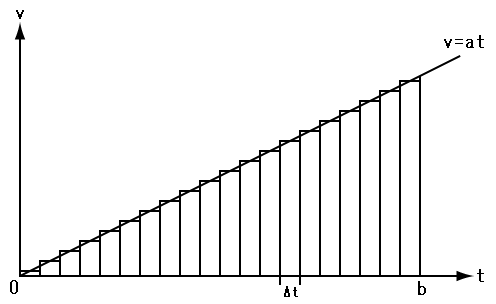
Figure6
Next, we shall consider the relationship between the average speed and the integral. Figure 6 shows the velocity-time graph of the uniformly accelerated motion.
Figure6
Let us calculate the area under the velocity-time graph in the interval time 0 to time b. It represents the distance x. Firstly, we divide the interval [0,b] into n subintervals: Δt=b/n. Secondly, we calculate the average speed of m-th subinterval: vm=ab(2m-1)/2n. Thirdly, we calculate the area of m-th thin rectangle. Its width is Δt=b/n, and its height is the average speed: vm=ab(2m-1)/2n. Finally, we calculate the total distance x:
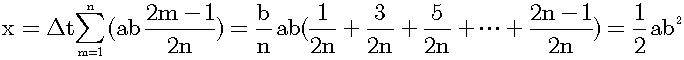
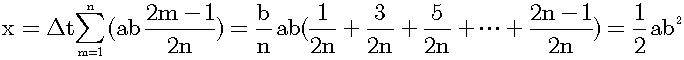
Therefore, the average speed is useful for the integration. That is, the average speed is the elemental concept.
As mentioned above, Δt is not zero but a very small value. This is the definitive difference between the average speed and the differential coefficient. In the above example, it is derived by the next equation: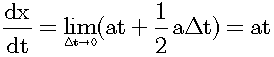
As mentioned above, Δt is not zero but a very small value. This is the definitive difference between the average speed and the differential coefficient. In the above example, it is derived by the next equation:
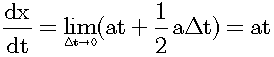
Even though 1/2(aΔt) approaches zero without limit, it doesn't equal zero. Within Euclidean space, Δt is only a very small value. Why do we ignore it for obtaining the differential coefficient? The cause may be that Newton was a physicist. He easily discarded Δt without hesitation because he wanted to apply the equation to the real world. So physics requires significant figures because all calculation results must be rounded to terminating decimals. Because terminating decimals can be easily converted to natural numbers, the rounding is digitization. So, only digitized data can be applied to the real world. That is, digitization is the indispensable step of physics.
In contrast, Δt is absolutely not zero in Euclidean space. If we assume that the position of the object at time t is x(t), the next equation represents the average speed of the object: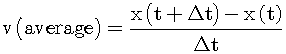
If Δt is zero, the above formula is indefinite. The differential and the integral are impossible without the average speed. Hence, we can discard Δt only in the final stage, in which we apply the result of the calculation to the real world. Only digital data can be applied to the real world.
Reversely, we can get only the digital data from the real world. Because we cannot directly observe the moving object, we can know only the position of it at a time.
In the digital space, irrational number must be approximated by terminating decimals. If a sequence
Figure7
In contrast, Δt is absolutely not zero in Euclidean space. If we assume that the position of the object at time t is x(t), the next equation represents the average speed of the object:
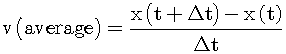
Reversely, we can get only the digital data from the real world. Because we cannot directly observe the moving object, we can know only the position of it at a time.
In the digital space, irrational number must be approximated by terminating decimals. If a sequence
Figure7